Area Moments of Inertia by Integration
Moments of Inertia (both area and mass) can be difficult to understand — or remember. This module and those to come will help you work through the concepts and calculations for area moments of inertia.
Materials:
- 12-inch wooden ruler
- 3D printer with flexible materials
- 3 straight pins or nails
- Reading: Area Moment of Inertia Background and Motivation (3 pages)
- Video: https://youtu.be/omrmA-QGkcw (7 minutes)
- Hands-on: Bend your ruler. There are three axes: one along the length, one along the inch-marks, and one through the thickness. Remember that when we’re talking about bending something, the axis you’re bending about is where your thumb would be. So a moment along the length of the beam twists the beam. A moment in either of the other two axes (flat-wise or width-wise) bends the ruler.
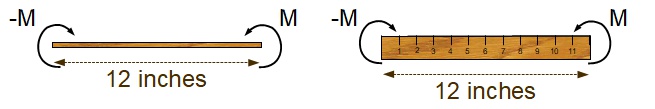
- Which way bends more easily?
- Reading: Note about Axes (1 page)
- Draw axes along your ruler so that z is along the beam. (Make your axes a right-handed coordinate axis system. If you look at the cross-section, you should see a regular x-y coordinate axes system.)
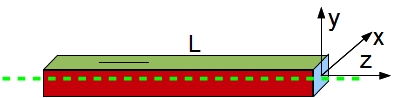
- Which moment bends more, the one about the x-axis or the one about the y-axis?
- Which way would you want to install the ruler in a structure to hold up more weight?
- Since the material and the length don’t change, what does?
- Draw axes along your ruler so that z is along the beam. (Make your axes a right-handed coordinate axis system. If you look at the cross-section, you should see a regular x-y coordinate axes system.)
- Reading: Ruler Bending About its Own Centroid (just over 1 page)
- Example (read or watch): Rectangular Beam Bending about Centroidal Axes (2 pages) or https://youtu.be/BvEu0fpLfdc (just over 1 minute)
- Write a brief paragraph for your own notes explaining the axes and the bending loads to ruler in your own hands.
- Print the 3D flexible i-beam.stl. Print this at 100% density with flexible material.

- If funds permit, print a copy with inflexible material so you can feel the difference.
- Hands-on: Bend the I-beam in your own hands in two directions.
- Draw the axes directly onto your printed beam so that the z axis is along your beam. Alternately, put pins into your beam so that you can see where the axes are. (Make sure it’s a right-handed coordinate system so that when you look at the cross-section you see a regular x-y axis system.)
- Draw an FBD of your beam to specify which direction your loads are acting in when you bend the beam in each of the directions. Relate your loads to a simply supported-beam.
- Which way does the beam bend more? About which axis is that? (Remember the direction the moment is applied is where your thumb points.)
- Which area moment of inertia are we talking about for each bending direction? (Ix and Iy)
- Hands-on: Draw a one-inch line on the top and bottom of the I-beam. Bend the I-beam about the x-axis. Note that one of your inch lines is longer than the other side.
- Reading: Neutral Axis (1 page)
- Video: watch the video animation of the stress in the bending I-beam from both directions. Bending as an I-beam and bending the same beam as an H-beam.
- Lay your printed I-beam on top of your pencil so you can push down on either side and bend the beam over the pencil as is shown in the video.
- Which direction deflects more easily?
- Example: Rectangular Beam Bending About Baseline (2 pages) or https://youtu.be/nD1ZMlrgJ_k (2 minutes)
- Hands-on: Lay your flexible I-beam flat on the table. If you push on the top two ends, the beam experiences a bending moment; the top surface of the beam will bend a bit but the bottom surface can’t deform. The neutral axis is where the deformation is zero.
- Write a brief paragraph for your own notes explaining why the moment of inertia about a rectangle’s baseline is bigger than about its centroid. Relate this to the ruler and your I-beam.
- Reading: Parallel Axis Theorem (1 page)
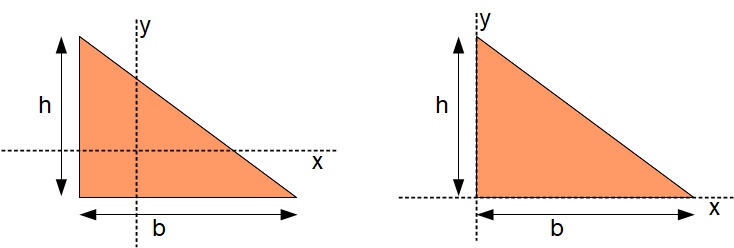
- Practice: Find the moment of inertia of the triangle about its baseline. Solution (watch only after you’ve worked it yourself): https://youtu.be/UjC4xjr0jCc (2 minutes)
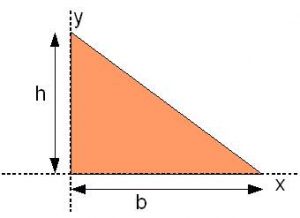
- Relate this to a triangular beam in your head where you are trying to bend a beam with a triangular cross-section which is also sitting on a table.
- Practice: think about what would be required to find the area moment of inertia about the centroidal axes of a triangle. Solution: https://youtu.be/MApovKX7CIc (just over 4 minutes)
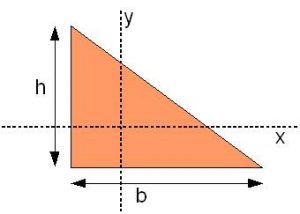
- Explain to yourself why the moment of inertia about the centroid of the shape is lower.
- Practice: use the parallel axis theorem to relate the moment of inertia about the baseline in #17 to the moment of inertia about the centroid in #18. Solution (1 page)
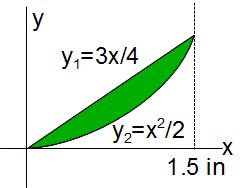
- Practice: Find the moment of inertia for the green shape about the x and y axes. The units shown are in cm; the drawing is not to scale. Solution: Area Between Two Curves (2 pages).
- Practice: Find the moment of inertia for the turquoise shape about the y axis. The units shown are in inches; the drawing is not to scale.

- This would be an odd-shaped beam, admittedly, but if you can find the moment of inertia by integration for this shape, you should be in reasonable condition for any shape. Answer = 5.53×10^7 in^4.
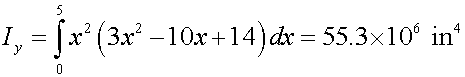
- Note: to find the moment of inertia about the x axis for this shape is complicated. (Students can sometimes get creative here. Be careful.)
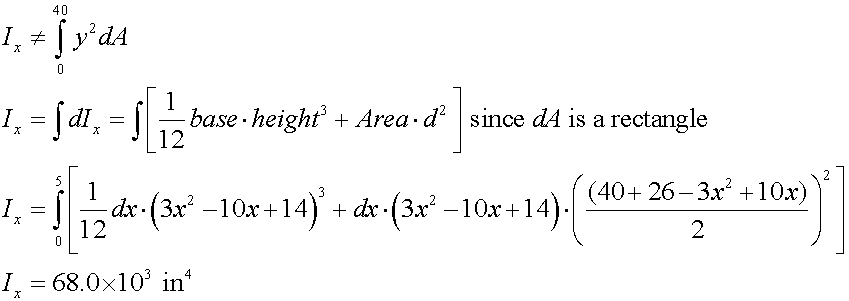
- This would be an odd-shaped beam, admittedly, but if you can find the moment of inertia by integration for this shape, you should be in reasonable condition for any shape. Answer = 5.53×10^7 in^4.
Once you can find the area moment of inertia by integration the next part is to learn the method of composite bodies. That will come in a future post.
